Harry Niquist was not wrong but is misunderstood

What

Synopsis

The most obvious method for determining the distortion of telegraph signals is to calculate the transients of the telegraph system.  This method has been treated by various writers, and solutions are available for telegraph lines with simple terminal conditions.  It is well known that the extension of the same methods to more complicated terminal conditions, which represent the usual terminal apparatus, leads to great difficulties.  The present paper attacks the same problem from the alternative standpoint of the steady-state characteristics of the system.  This method has the advantage over the method of transients that the complication of the circuit which results from the use of terminal apparatus does not complicate the calculations materially.  This method of treatment necessitates expressing the criteria of distortionless transmission in terms of the steady-state characteristics.  Accordingly, a considerable portion of the paper describes and illustrates a method for making this translation.  A discussion is given of the minimum frequency range required for transmission at a given speed of signaling.  In the case of carrier telegraphy, this discussion includes a comparison of single-sideband and double-sideband transmission.  A number of incidental topics is also discussed.

Telegraphy distinguished from other forms of electrical communication

1. The time is divided into approximately equal units
   which will be called time units.
   
2. There is a finite number of conditions,
   and each time unit is characterized by a single one of these conditions.

Nyquist rate

a value (in units of samples per second or Hertz, Hz) equal to twice the highest frequency (bandwidth) of a given function or signal.

Harry's sampling rate applies only to a continuous signal with a finite number of states

Consider audio

Consider music without transients

I would find that intensely boring, and will not address it.

Consider music with only a few allowed amplitude values.

I find that intensely unpleasant, and will not address it.

Consider sine waves

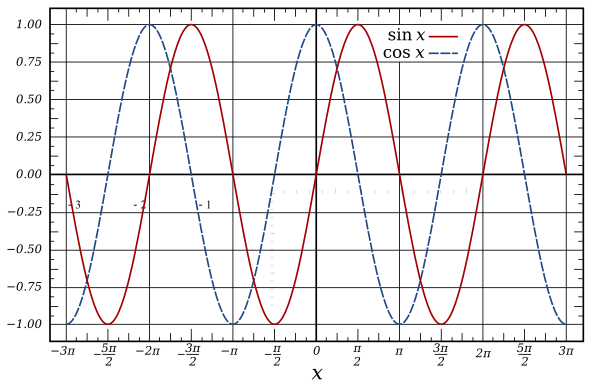
Sample that red plot at exactly twice per period, e.g. -π, 0 and π.  (result = 0).
This effect is precisely analogous to the problem of resolving black and white line pairs, where each pair comprises a cycle. Depending on the phase at which samples occur, the result may be featureless gray.
In order to ensure that all line pairs are reliably detected requires sampling at least 3 samples per cycle, with no confidence in actual amplitudes of original stimuli.
Again, these trivial examples address signals neither continuously varying nor aperiodic.
One known about human perception of music signals:  it is band-limited, meaning that amplitudes neither change faster than some maximum rate, nor do they change slower than some minimum rate. Another known about music perception is that amplitudes cannot be distinguished with greater than 16-bit resolution.

For the sake of argument, suppose that audio amplitudes may be sampled without loss of fidelity at a rate ten times its (20kHz) upper limit, so approximately 200kHz. The above equation suggests that capturing changes in signal (AKA sigma-delta or DSD) wants capturing with 31-bit resolution or perhaps 1-bit resolution at 20,000 times 200kHz or 4 GHz.
Since current technology makes either of those alternatives economically unattractive, shortcuts and misinformation (advertising technobabble) are employed.
In fact, human hearing cannot resolve 16 bits of amplitude at 20kHz.

An experiment could capture highly demanding (but interesting) audio at the highest possible sampling and amplitude resolution, then resampling that original at lower sampling and amplitude resolutions, playing back differences between those signals and discovering audibility thresholds. Practically, when such experiments are conducted e.g. for MP3, differences are most audible at musical transients, when Harry's steady-state condition least applies.