back

Microscope FundamentalsOther resources
GeneralitiesMicroscopes traditionally shared some mechanical conventions:
When microscope frames evolved from straight tubes to separate heads with prisms, accesories could be introduced between objectives and eyepieces, e.g. vertical illuminators and/or polarizing filters, with increased distance between finite eyepieces and objectives requiring lenses to restore parfocality. Infinitity objectives enable inserting accessories without parfocality corrections. These are typically optimized for some manufacturer's objectives optical formula. Many modern microscopes use other than RMS threads; here is a list. Here is a list of threads used in astronomy. Aberrations - spherical, chromaticMainly from incorrect geometries and diffraction changes with wavelength.
Aperture - effective/working, equivalent, pupil ratio, vs numeric (N.A.)
Conjugate focal planes - Compound microscope raysWorth watching: Abbe's experiments and conjugate planes
Correcting eyepieces or tube lensesUnlike e.g. Nikon or Olympus, Zeiss and Leica infinity objectives want tube lens corrections. The right combination of objective and eyepieceHigher objective magnifications are increasingly liable to optical aberrations, Notes:
As might be expected, a CFW eyepiece (applying no corrections) worked poorly with most Zeiss,
Coverslip thickness error impact vs N.A.
Systematic impact suggests mitigating modest aberrations (e.g. from wrong slide coverslip) DoF2 = DoF1 * (f/#2/f/#1) * (m1/m2)**2
diopter = 2 for 500mm fl
Floaters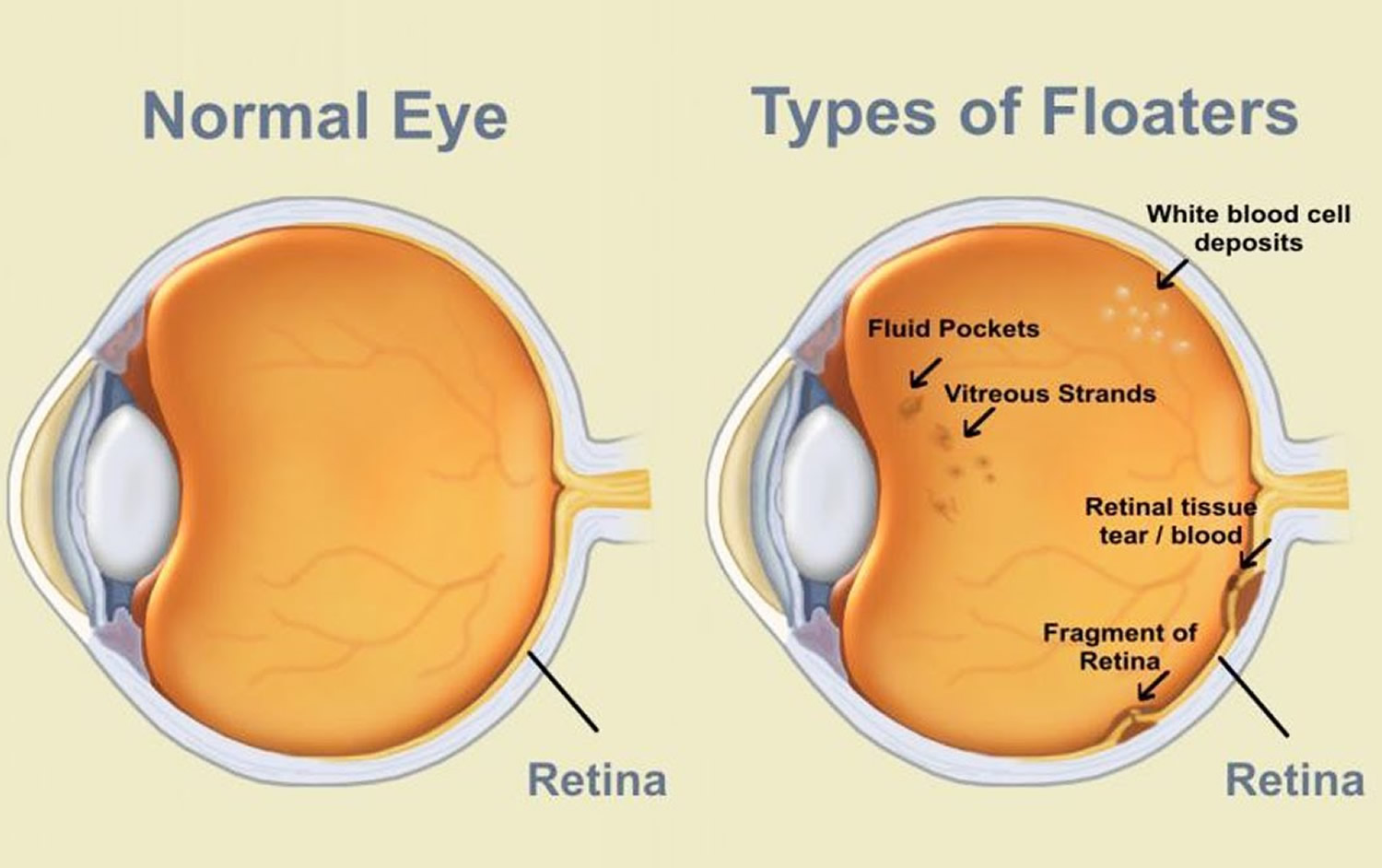 Vitreous Strands are liable to be illuminated. Different eyepiece relief can move Lamp Filament conjugate plane, affecting floater visibility. Illumination- internal vs external; brightfield vs darkfield- Köhler illumination - diascopic (thru specimens) vs episcopic (above objects):  compound microscope with both episcope and diascopic illumination Lens formulaesimple1/f = 1/do + 1/di {1} di becomes
f for infinite do
m = di/do {2}
zero magnification for lens focused @ infinity
magnification change by focus distance f = (d2 - d1)/(m2 - m1); {3} alternatively:
d2 = d1 + f*(m2 - m1)
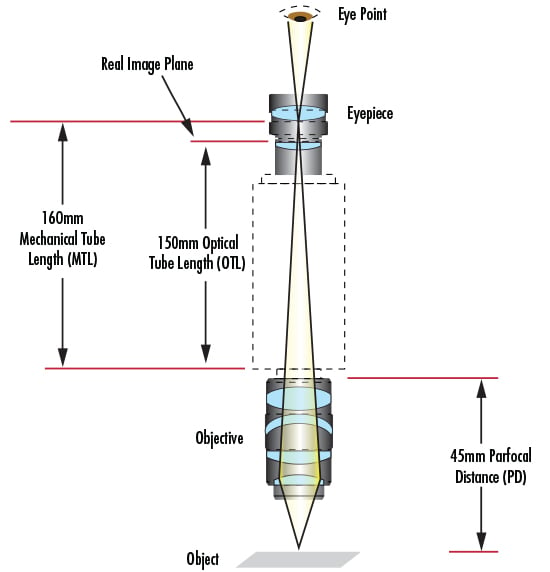
m2 = m1 + (d2 - d1)/fmagnification for classic (RMS) compound microscope m = (L/fo)*(D/fe),...where: m = magnification
L = tube length (160mm)
D = normal vision relaxed distance (250mm)
f = focal length
fo = objective focal length
fe = eyepiece focal length
di = lens to image distance
do = lens to object distance
For 160mm tube length, a 10x objective has 16mm focal length and a 10x eyepiece has 25mm focal length. For infinity scopes, substitute "tube lens focal length" for "tube length". Olympus infinity objectives expect 180mm tube lens focal length; Nikon finite CF BD and M Plan objectives expect 210mm tube length. Objectives: Finite vs infinityBill Otto explains lenses and ray diagramsObjective resolving power depends only on N.A., not magnification A 20x 0.75 infinity objective at 40x with a 400mm tube lens, has no degradation relative to a 40x 0.75 with a 200mm tube lens. At specified focal lengths, objectives vary by useful field circle diameters. Before 1980, 18mm was typical; modern Plan objectives can be 22mm or more.  Finite-conjugate microscope vs. infinite-conjugate microscope with tube lens. from: Systematic design of microscope objectives A finite objective's correction is designed for that tube length, with many objectives also depending on both coverslip glass and eyepiece for corrections. More explanationThe upper diagram approximates (RMS == Royal Microscope Society) microscopes;with Pupil also called objective's rear conjugate or back focal plane.The lower diagram also applies for some modern finite microscopes, with Objective + Infinity space + Tube lens combined as a compensated "finite" objective.While infinity objectives may be used with a tube lens of any focal length, specified magnification depends on that focal length. Contrast and non-image-forming light.While lenses focus images on your retina or other sensor,they do not prevent other photons from also stimulating sensors. When viewing a three-dimensional scene, perhaps focusing on a near object, photons scattered from more distant objects may also land on the same photosensors. Properly (Köhler) aligned conjugate image and illumination planes also improve contrast. Some non-image-forming light can be blocked by an iris diaphragm, as in this diagram:  Ignore Microlens Array. Relay part is afocal photography, where Field Lens is the eyepiece or ocular.
Objective standards - DIN: 45mm parfocal distance
Vignetting - infinity microscopeRays from an infinity objective are only parallel when from a single point;with increasing distance between objective and field lens, a larger field lens is needed to avoid vignetting:  An objective's back focal plane is where parallel rays entering that objective focus. | |||||||||||||||||||||||
|
maintained by blekenbleu |